Arduino 的 Starter-Kit Project,跟著試做已經進行到第5個教學例子。自從跟身邊朋友講起之後,原來也有些朋友有玩過Arduino,有學過電子的同事,學電腦設計的舊同學,點子活動中的新相識,都對這個有點認識。只是大概網上資源香港還是不多,主要仍然是台灣人架的網站,書店和圖書館也有少數台灣書可以找到。而香港除了我入手的RS Components外,還有深水埗黃金對面的福仁商場G37-Tell How Technology有賣。有一個叫Dim Sum Lab 的空間可以讓香港的同好交流,有點像Maker Bay的形式,但是不同的主題。
Arduino 是一塊電路板和編程語言的整合。但它卻讓很多沒有任何電工或編程經驗的人也可以開始動手做電子硬體的控制。它也是作為一個開源項目,讓社群的人可以在它的基礎上改善和發展,出現後推動了一股稱為自做者/創客的文化。它在電路上整合了微控制器(例如Arduino Uno上的ATmega328P),輸入輸出介面(各種Pin位、USB接口);當結合各種電子元件(如開關、感測器、LED、步進馬達),和配合Arduino語言(類似C)的程式開發環境,便可以嘗試自做一些電子機器。而特別令我感興趣的,是它讓自己可以連繫起軟體和硬體。看到網上的高手可以自行開發出很酷的東西:
<駭客只要用這個USB充電器,就可以竊取你的無線鍵盤輸入資料>
http://www.techbang.com/posts/21946
<將Arduino 變成Game Boy,還可自行設計遊戲的Arduboy>
http://www.techbang.com/posts/23764
<什麼樣的工程師能上太空?13 歲少年玩 Arduino,玩到被送上太空!>
http://buzzorange.com/techorange/2013/10/14/thirteen-year-olds-hack-their-way-into-space/
<簡易Arduino機器人製作>
http://www.makezine.com.tw/make2599131456/arduino13
說它是開源項目因為當初開發團隊的決定是開放這個項目的設計,只有Arduino這個名稱、標誌以及圖案是受保護的商標(不過,現在有關於 arduino.cc和 arduino.org的分別)。硬件的電子連接都是在創意共享Creative Common Attribution Share-Alike 授權條款去公開原設計文件,可以讓人模仿、以至修改成自己所需的底板或相容系統,他們的網頁上就有教如何自製一塊Arduino。就不同的需要,它們自家開發的就有初學者入手的Arduino UNO、細小便攜的Arduino Mini、可穿戴和縫紉在衣服上的LilyPad Arduino、有WIFI和增強了運算能力Arduino Yun等,其他人仕自行開發的有Intel Galileo, Webduino, 等。Arduino的社群中,在底板以上還有著不同的擴充板(Shield)可以擴充它的功能,如Motor Shield、Ethernet Shield等。而程式方面,用家可以在提供的IDE介面自行編寫控制程式(Sketch),而且還有各種的函式庫可以引用或自建。
Bertrand Russell: "Three passions, simple but overwhelmingly strong, have governed my life: the longing for love, the search for knowledge, and unbearable pity for the suffering of mankind."
2016年5月29日 星期日
2016年5月21日 星期六
Edx - TW3421x Credit Risk Management
Edx 上看到一個Credit Risk Management的課堂,報了打算讓自己溫習一下從前上課所學。最近這快要完成了,來總結這課堂所學的內容。
這課堂由Delft University of Technology的Dr. Pasquale Cirillo 講授。說話速度像是刻意放慢了,講解不會沉悶之餘,初時還有用RSA動畫的方式去解釋事情之間關係。內容方面,沒有涉及複雜的數學證明,某些公式出現時就重申:推導過程不在課程以內,然後直接使用。這令課程變得簡單之餘,也清晰了這是集中在讓初學者理解概念。
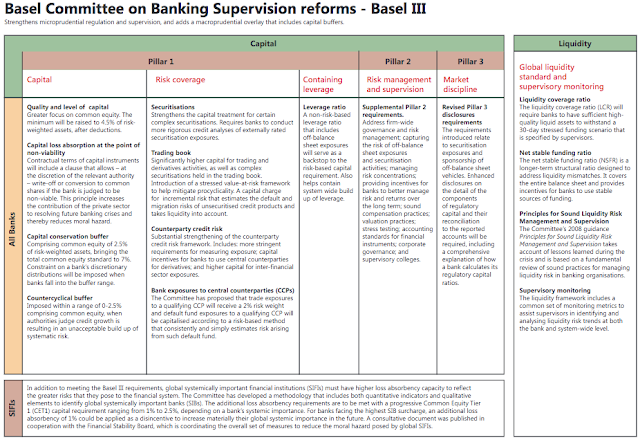
課程把信用風險放在從巴塞爾協定中開始講起。巴塞爾協定是對銀行業的其中一項重要條約。從巴塞爾協定二起,基本定立出三條支柱。
1) Minimum Capital Requirement (Credit Risk, Market Risk, Operational Risk)
2) Supervisory Review Process
3) Market Discipline
更仔細的在:http://www.bis.org/bcbs/basel3/b3summarytable.pdf
這課堂由Delft University of Technology的Dr. Pasquale Cirillo 講授。說話速度像是刻意放慢了,講解不會沉悶之餘,初時還有用RSA動畫的方式去解釋事情之間關係。內容方面,沒有涉及複雜的數學證明,某些公式出現時就重申:推導過程不在課程以內,然後直接使用。這令課程變得簡單之餘,也清晰了這是集中在讓初學者理解概念。
The computation of WCDR is performed using the formula you see on your screen. I do agree with you if you think that this formula has somehow fallen from the sky.
That's true: in this course this formula has fallen from the sky. The point is that, in order to derive this formula completely and formally, we would need - all - a big probabilistic apparatus that we do not have, such as for example the copula model. So, that's it: just take this formula for granted.
課程把信用風險放在從巴塞爾協定中開始講起。巴塞爾協定是對銀行業的其中一項重要條約。從巴塞爾協定二起,基本定立出三條支柱。
1) Minimum Capital Requirement (Credit Risk, Market Risk, Operational Risk)
2) Supervisory Review Process
3) Market Discipline
更仔細的在:http://www.bis.org/bcbs/basel3/b3summarytable.pdf
2016年5月8日 星期日
生活雙週 - 空手道, 魚仔板, Udemy, Arduino
這兩星期為之後的日子突然又下了幾個決定/行動。
同事推介一起上柔術的課,正正讓我面對一直在意的一個主意:重新空手道的練習。自從某天在地鐵上遇到大昭師兄後,大概都有了回去的決心。今晚剛剛回去了空手道的練習,身體和技術都未有怎樣生疏;征遠鎮和拔塞大的動作練幾次也記得了;但只有之前也記不上的那些套拳分解,仍是忘了大半。早兩年一直有為自己定下一些目標,但大概受著擔心和討厭今年就算定下了,也未會實踐這個目標,而一直未為今年打算。但現在開始了,這就好了。想做又應該做的事,不應該因為害怕令自己停步,「怯,你就輸成世」。
在Skatecity買了塊平價的Street牌魚仔板,晚上到吐露港沿單車徑旁的行人路試踩。記得是焜哥和店員所講的都是踩著前面釘位,不過第一晚試踩並不容易,人的重心和滑板的移動總是不配合。學習時未想在單車路上,行人路是紅磚式的地面,隙縫的阻力也很大,不斷只有幾步幾步距離地移動。到有個位置是旁邊有休憩處的,那地面就沒那麼粗糙,合適得多,試過這段路後,沿行人路回去時也順了點,後腳也放到板上。之後放在家時找些YouTube上的penny教學,記得幾段基本滑行、轉彎、Tictap。前晚就去了另一個公園的緩跑徑練習,慢慢繞過一圈後就感覺開始掌握到平衝感。然後繞了幾圈到凌晨才回家。今早到附近「觀星台」的空地練習,算每一次嘗試上板/滑前/轉彎(右)都可以了。
PMP 的 35 contact hours, 終於在Udemy 找到平價之選,LearnSmart LLC的Project Management Professional,只要 USD$20。標榜是PMI的Registered Education Provider (R.E.P.),完成課程後的證書可以作為報PMP考試要求的35 Contact hour 。 影片的講解尚算有條理及清晰,還可以在手機App下載起來,然後在上下班時去看,暫時完成了13%的進度。因為自己上年在考慮的時候己經把圖書館借來的書看完一次,不是只靠它的影片開始從零學習,所以只算是在用來覆習和要知道PMBOK5更新的部分。如果要備試的話我覺得更重要的還是做練習,現在尚未看它的習題,下載起首幾課的補充資源中就都有包括crossword puzzle/ flash card / quiz 等等,大概都是之後自學都會用的。
在看工聯會除了同事介紹的柔術外還有什麼課程時,自己又想找一些電子工程的知識學習。看到有教授Arduino的課堂,想起早幾天在圖書舘看過這名字的,於是再找想關的介紹或學習。找到其他電工會的課程也差不多價錢,而且連零件實習的還另需零件的費用,當想找找那裡可以買到時,原來官方也有出一套Starter Kit, 有一塊Arduino UNO, 可以跟著學習的Projects Book和相關電子零件等。在RS 這個電子零件商入手買了。不知是否香港不算著普及,少有個人提及Arduino,下單後也因為RS香港未有貨,而要等海外運送。在一個星期後終於送到屋企,相比電話聯絡時他們預估的快了兩天。
最後,還有7月義大利之行的機票,比之前搜尋時貴了,不過決定還是會去的。這個工作營從知道的一刻,一直在一個兩難的選擇的猶豫中,因為日子可能跟工作上的一個專案相撞。不過經番思量,這個工作上的機遇,就當凡事留一線吧。義大利:作為一直想看看的歐洲城市,一次非工幹的旅行,期望多些新鮮體驗吧。
同事推介一起上柔術的課,正正讓我面對一直在意的一個主意:重新空手道的練習。自從某天在地鐵上遇到大昭師兄後,大概都有了回去的決心。今晚剛剛回去了空手道的練習,身體和技術都未有怎樣生疏;征遠鎮和拔塞大的動作練幾次也記得了;但只有之前也記不上的那些套拳分解,仍是忘了大半。早兩年一直有為自己定下一些目標,但大概受著擔心和討厭今年就算定下了,也未會實踐這個目標,而一直未為今年打算。但現在開始了,這就好了。想做又應該做的事,不應該因為害怕令自己停步,「怯,你就輸成世」。
在Skatecity買了塊平價的Street牌魚仔板,晚上到吐露港沿單車徑旁的行人路試踩。記得是焜哥和店員所講的都是踩著前面釘位,不過第一晚試踩並不容易,人的重心和滑板的移動總是不配合。學習時未想在單車路上,行人路是紅磚式的地面,隙縫的阻力也很大,不斷只有幾步幾步距離地移動。到有個位置是旁邊有休憩處的,那地面就沒那麼粗糙,合適得多,試過這段路後,沿行人路回去時也順了點,後腳也放到板上。之後放在家時找些YouTube上的penny教學,記得幾段基本滑行、轉彎、Tictap。前晚就去了另一個公園的緩跑徑練習,慢慢繞過一圈後就感覺開始掌握到平衝感。然後繞了幾圈到凌晨才回家。今早到附近「觀星台」的空地練習,算每一次嘗試上板/滑前/轉彎(右)都可以了。
PMP 的 35 contact hours, 終於在Udemy 找到平價之選,LearnSmart LLC的Project Management Professional,只要 USD$20。標榜是PMI的Registered Education Provider (R.E.P.),完成課程後的證書可以作為報PMP考試要求的35 Contact hour 。 影片的講解尚算有條理及清晰,還可以在手機App下載起來,然後在上下班時去看,暫時完成了13%的進度。因為自己上年在考慮的時候己經把圖書館借來的書看完一次,不是只靠它的影片開始從零學習,所以只算是在用來覆習和要知道PMBOK5更新的部分。如果要備試的話我覺得更重要的還是做練習,現在尚未看它的習題,下載起首幾課的補充資源中就都有包括crossword puzzle/ flash card / quiz 等等,大概都是之後自學都會用的。
在看工聯會除了同事介紹的柔術外還有什麼課程時,自己又想找一些電子工程的知識學習。看到有教授Arduino的課堂,想起早幾天在圖書舘看過這名字的,於是再找想關的介紹或學習。找到其他電工會的課程也差不多價錢,而且連零件實習的還另需零件的費用,當想找找那裡可以買到時,原來官方也有出一套Starter Kit, 有一塊Arduino UNO, 可以跟著學習的Projects Book和相關電子零件等。在RS 這個電子零件商入手買了。不知是否香港不算著普及,少有個人提及Arduino,下單後也因為RS香港未有貨,而要等海外運送。在一個星期後終於送到屋企,相比電話聯絡時他們預估的快了兩天。
最後,還有7月義大利之行的機票,比之前搜尋時貴了,不過決定還是會去的。這個工作營從知道的一刻,一直在一個兩難的選擇的猶豫中,因為日子可能跟工作上的一個專案相撞。不過經番思量,這個工作上的機遇,就當凡事留一線吧。義大利:作為一直想看看的歐洲城市,一次非工幹的旅行,期望多些新鮮體驗吧。
2016年5月1日 星期日
賭波的初哥方式-Elo Rating System 的理解
之前在未了解背後數學之前先嘗試個應用。今個周未有空就來了解一下Elo Rating System背後是什麼理論,和如何得出那樣的公式了。
Part A)機率
先來看看「邏輯函数」Logistic Function。在很多地方都會看到它的身影,例如物種的人口增長,統計學上的對True/False這類二元結果的回歸分析。
「邏輯函数」 有這樣的一般型式:$$y = \frac{L}{ 1 + e^{-k(x-x_0)} }$$
$e$ :自然對數
$x_0$:x 的中間值
$L$ :y 的最大值
$k$ :斜度
例子一:Standard Logistic Function:$y = \frac{1}{1 + e^{-x}}$
例子二:國際象棋界 USCF 的 Elo rating system 的勝率期望值:$y = \frac{1}{1 + 10^{-\frac{1}{400}(r_A-r_B)}}$
我們考慮代入的是「分數差」(甲的分數-乙的分數), 即是$x=(r_A-r_B)$,$x_0=0$。一個函數可以作為「分數」 與「勝負機率」的轉換,大概很多$\mathbb{R} \to (0,1)$ 的函數都可以做到。而這「邏輯函数」還有以下特質::
「邏輯函数」 在統計模型的重要性在於與「邏輯迴歸」Logistic Regression 的關係。
Logistic Regression Model與一般的「簡單線性迴歸」 Ordinary Linear Regression都是屬於GLM的其中一員,分別在於對「應變數」Dependent Variable的分佈,和所謂的「連結函數」Link Function有不同假設。Logistic Regression Model中,Y 的分佈是要配合"勝/負"這類二元結果, 連結函數的不同就得出機會率可以寫成Logistic Function的形式。Logistic Regression :
$$logit( E [Y | X] ) = ln(\frac{p}{1-p}) = \beta X$$
對觀察值Y的分佈假設為 $Y \sim Binomial (1 , p) $。上式經過移項後會得到:$p = \frac{1}{1 + e^{-\beta X}}$,也就是開始時所見的Logistic Function的形式。
終於,我們回來看看Elo Ratings中的機率公式:
$$S_{expect} = \frac{1}{1 + 10^{-\frac{1}{400}(r_A-r_B)}}$$
Part B)分數
每名棋手會有一個初始分數$r_0$,然隨著實際對賽的結果,用以下公式更新棋手成積:
$$r_{post} = r_{pre} + K (S_{actual} - S_{expect})$$
$r_{post}$:對賽後棋手經調整後的分數。
$r_{pre}$:對賽前棋手原來的分數。
$S_{actual}$:實際結果,簡單可以設定:贏=1分,輸=0分,和=0.5分。
$S_{expect}$:預期結果,就是PartA計算甲會贏的機率公式。
$K$:這一般稱作attenuation factor,是調整新結果的影響和原有分數之間的比重。
一般會有這些考慮:假設比賽結果對新手影響較大,假設重要比賽的影響較大。
因為兩個等級的選手對賽,可以預期分數高的有較大贏面。棋手的分數要值得調整,他應該要表現得超越自己原有等級所預期的水準。Elo Rating更新分數的公式的設計就是為了達到這個效果。
另外,例如有 1200分的棋手A 和 1000分的棋手B 比賽:A,B的預期贏面分別算出是76%, 24%。 A勝出只會增加$0.24K$的分數,B勝出卻會增加$0.74K$的分數。所以:贏(輸)了該贏(輸)的比賽,分數不會有大幅調整;但如果出現戲劇性的結果,分數的調整就會較大。
Part C)應用
這套Elo Rating System在以下幾方面都有被應用:
遊戲:
League Of Legends
http://leagueoflegends.wikia.com/wiki/Elo_rating_system
國際象棋界:
World Chess Federation (FIDE)
https://www.fide.com/fide/handbook.html?id=172&view=article
足球:
World Football Elo Ratings
http://www.eloratings.net/system.html
FIFA Women's World Rankings
http://www.fifa.com/worldranking/procedureandschedule/womenprocedure/index.html
http://resources.fifa.com/mm/document/fifafacts/r%26a-wwr/52/00/99/fs-590_06e_wwr-new.pdf
Footballdatabase.com (雖然無提供背後的模型,但如果沒有數據作自行測試的話也可以一看)
http://footballdatabase.com/ranking/europe/1
因為各方面的比賽有不同特質,所以模型參數略有不同。用以上的 FIFA Women’s World Ranking (WWR) 的模型去看足球方面的實際運作(這裡修改了官方符號方便表示):
$$S_{expect} = 1 / (1 + 10^{x/2})$$
$$ r_{new} = r_{old} + K ( S_{actual} - S_{expect} )$$
文件中稱當中 $x = [r_A - r_B] / (\text{scaling factor})$。scaling factor是為了令新隊伍從1000分開始;對賽中每100分的差距做成64%的的機會勝出。用Excel模擬一下會得到它的scaling factor = -200,所以一樣是這條式:$S_{expect} = 1 / (1 + 10^{-\frac{1}{400}(r_A-r_B)})$



------------
最後一部份,我是懷疑是否有關的,是這套評分和Exponential Distribution的關係。
因為:$A, B \sim Exp(1) \Rightarrow x_0 - \beta ln(A/B) \sim Logistic(x_0, \beta)$
設$R_A, R_B \sim Exp(\dot)$ A,B 是某種實力的量度。Exponential distribution 的圖明顯與Normal Distribution 不同的,它假設選手的$R_A, R_B$ 大多是在低實力區,高手則愈來愈少。它還有一個特點,是分佈上的「無記憶性質」(Memoryless):$Pr(X>m+n|X>m) = Pr(X>n)$ 。對給定的任意一個參考分數而言,比你高同樣n級的比例是一樣的。用一個效果比喻:無論是在哪一級的角色,在下一個等級之前,總是有面前的人當中最弱的3%等著你去超越。
( 以$Exp(1/30)$為例。平均等級是30級。R:pexp(1, rate=1/30) )
設$R_a=ln(R_A), R_b=ln(R_B)$ 。用$ln()$將實力的比例尺轉變成方便比較的分數,$log()$這個運算的起源,是當年在未有計算機的發明之前,有一樣叫對數表的工具,為了方便計算大數的乘法。
$a-b = ln(exp(Ra-Rb)) = ln(exp(Ra)/exp(Rb)) = ln(A/B) \sim Logistic(0,1)$
這就得出分數差會符合Logistic Distribution.
但這是否有什麼意義呢?未想清楚。。。
------------
Part A)機率
先來看看「邏輯函数」Logistic Function。在很多地方都會看到它的身影,例如物種的人口增長,統計學上的對True/False這類二元結果的回歸分析。
「邏輯函数」 有這樣的一般型式:$$y = \frac{L}{ 1 + e^{-k(x-x_0)} }$$
$e$ :自然對數
$x_0$:x 的中間值
$L$ :y 的最大值
$k$ :斜度
例子一:Standard Logistic Function:$y = \frac{1}{1 + e^{-x}}$
例子二:國際象棋界 USCF 的 Elo rating system 的勝率期望值:$y = \frac{1}{1 + 10^{-\frac{1}{400}(r_A-r_B)}}$
我們考慮代入的是「分數差」(甲的分數-乙的分數), 即是$x=(r_A-r_B)$,$x_0=0$。一個函數可以作為「分數」 與「勝負機率」的轉換,大概很多$\mathbb{R} \to (0,1)$ 的函數都可以做到。而這「邏輯函数」還有以下特質::
- 這函數可以輸入實數的「分數差」,而輸出0到1之間的機率值;而且數值是不斷上升的,所以差異愈大,贏(輸)機率就愈大。(這兩個特質就適合用來作"分數差" 和"輸贏機率"之間的轉換)
- 零作為中間點是反向對稱的 $Pr(x)=1-Pr(-x)$,高分方的勝率等於低分方的負率。當雙方實力相等,也就是"分數差"在等於零的時候,輸贏的機率是0.5。
- 而差異愈接近零的時候機率的變化的速度較大;但差異愈大的時候,這個機率的變化速度就愈不明顯。(這個有點像經濟學上「邊際效益遞減」的概念,現實上有點猶豫)
「邏輯函数」 在統計模型的重要性在於與「邏輯迴歸」Logistic Regression 的關係。
Logistic Regression Model與一般的「簡單線性迴歸」 Ordinary Linear Regression都是屬於GLM的其中一員,分別在於對「應變數」Dependent Variable的分佈,和所謂的「連結函數」Link Function有不同假設。Logistic Regression Model中,Y 的分佈是要配合"勝/負"這類二元結果, 連結函數的不同就得出機會率可以寫成Logistic Function的形式。Logistic Regression :
$$logit( E [Y | X] ) = ln(\frac{p}{1-p}) = \beta X$$
對觀察值Y的分佈假設為 $Y \sim Binomial (1 , p) $。上式經過移項後會得到:$p = \frac{1}{1 + e^{-\beta X}}$,也就是開始時所見的Logistic Function的形式。
終於,我們回來看看Elo Ratings中的機率公式:
$$S_{expect} = \frac{1}{1 + 10^{-\frac{1}{400}(r_A-r_B)}}$$
- 從 $e$ 變成 10的次方:因為 $10^x = {e^{ln(10)}}^x =e^{ln(10)x} $,這只是在$k$值的影響。
- $k$:1/400,這個斜度是雙方選手的分數差如何轉換到 0-1的比例上。例如當同樣估計為A勝B,但估計的機率是60%還是70%就是這k值影響到。在線性回歸中我們會用OLS的方法去求取參數,在 Logistic Regression中參數是用「最大似然估計」Maximum Likelihood Estimation (MLE)找出來。
- $r_A, r_B$:選手的分數,這裡並不是一個可以直接觀察到的自變數,如何得出這分數就是Elo Rating 的另一重要部份。
Part B)分數
每名棋手會有一個初始分數$r_0$,然隨著實際對賽的結果,用以下公式更新棋手成積:
$$r_{post} = r_{pre} + K (S_{actual} - S_{expect})$$
$r_{post}$:對賽後棋手經調整後的分數。
$r_{pre}$:對賽前棋手原來的分數。
$S_{actual}$:實際結果,簡單可以設定:贏=1分,輸=0分,和=0.5分。
$S_{expect}$:預期結果,就是PartA計算甲會贏的機率公式。
$K$:這一般稱作attenuation factor,是調整新結果的影響和原有分數之間的比重。
一般會有這些考慮:假設比賽結果對新手影響較大,假設重要比賽的影響較大。
因為兩個等級的選手對賽,可以預期分數高的有較大贏面。棋手的分數要值得調整,他應該要表現得超越自己原有等級所預期的水準。Elo Rating更新分數的公式的設計就是為了達到這個效果。
另外,例如有 1200分的棋手A 和 1000分的棋手B 比賽:A,B的預期贏面分別算出是76%, 24%。 A勝出只會增加$0.24K$的分數,B勝出卻會增加$0.74K$的分數。所以:贏(輸)了該贏(輸)的比賽,分數不會有大幅調整;但如果出現戲劇性的結果,分數的調整就會較大。
Part C)應用
這套Elo Rating System在以下幾方面都有被應用:
遊戲:
League Of Legends
http://leagueoflegends.wikia.com/wiki/Elo_rating_system
國際象棋界:
World Chess Federation (FIDE)
https://www.fide.com/fide/handbook.html?id=172&view=article
足球:
World Football Elo Ratings
http://www.eloratings.net/system.html
FIFA Women's World Rankings
http://www.fifa.com/worldranking/procedureandschedule/womenprocedure/index.html
http://resources.fifa.com/mm/document/fifafacts/r%26a-wwr/52/00/99/fs-590_06e_wwr-new.pdf
Footballdatabase.com (雖然無提供背後的模型,但如果沒有數據作自行測試的話也可以一看)
http://footballdatabase.com/ranking/europe/1
因為各方面的比賽有不同特質,所以模型參數略有不同。用以上的 FIFA Women’s World Ranking (WWR) 的模型去看足球方面的實際運作(這裡修改了官方符號方便表示):
$$S_{expect} = 1 / (1 + 10^{x/2})$$
$$ r_{new} = r_{old} + K ( S_{actual} - S_{expect} )$$
文件中稱當中 $x = [r_A - r_B] / (\text{scaling factor})$。scaling factor是為了令新隊伍從1000分開始;對賽中每100分的差距做成64%的的機會勝出。用Excel模擬一下會得到它的scaling factor = -200,所以一樣是這條式:$S_{expect} = 1 / (1 + 10^{-\frac{1}{400}(r_A-r_B)})$

- 它們對模型的修改上考慮到入球數目的不同:

- 主場的優勢:主隊加100分
"A glance at the historical results shows that teams perform better at home than away; the home teams keep 66% of the points, while the opponents return home with 34%. To neutralise this effect, a correction is made by enhancing the rating of the home team by a value of 100 points (corresponding to 64%)."
- 對於賽事重要性:

- 參考的時間歷史:45年的比賽紀錄,在評分的角度上還可以接受,但我覺得對勝負機會率的目的來說就太多。現在的球隊隊員跟好幾年前的早就不同了吧。
"Solid foundation: some 6500 games since 1971"
- 開始評分所需的數據:其實我覺得這套方式比較適合LOL遊戲平台上的計分,那時每次分數更新反映的是一個學習過程。但在象棋/足球這類大量練習,然後參加一場聯賽的情況中,每次分數更新就像是尋求反映真正實力的過程,這就要有足夠對實往績能達到效果。事實上,也因為Logistic Regression 的參數是用到MLE的方法,一般需要的樣本數也要較大。
"The ranking of a team is deemed official when:They have played at least 5 matches against teams with an official ranking. etc..."
------------
最後一部份,我是懷疑是否有關的,是這套評分和Exponential Distribution的關係。
因為:$A, B \sim Exp(1) \Rightarrow x_0 - \beta ln(A/B) \sim Logistic(x_0, \beta)$
設$R_A, R_B \sim Exp(\dot)$ A,B 是某種實力的量度。Exponential distribution 的圖明顯與Normal Distribution 不同的,它假設選手的$R_A, R_B$ 大多是在低實力區,高手則愈來愈少。它還有一個特點,是分佈上的「無記憶性質」(Memoryless):$Pr(X>m+n|X>m) = Pr(X>n)$ 。對給定的任意一個參考分數而言,比你高同樣n級的比例是一樣的。用一個效果比喻:無論是在哪一級的角色,在下一個等級之前,總是有面前的人當中最弱的3%等著你去超越。
( 以$Exp(1/30)$為例。平均等級是30級。R:pexp(1, rate=1/30) )
設$R_a=ln(R_A), R_b=ln(R_B)$ 。用$ln()$將實力的比例尺轉變成方便比較的分數,$log()$這個運算的起源,是當年在未有計算機的發明之前,有一樣叫對數表的工具,為了方便計算大數的乘法。
$a-b = ln(exp(Ra-Rb)) = ln(exp(Ra)/exp(Rb)) = ln(A/B) \sim Logistic(0,1)$
這就得出分數差會符合Logistic Distribution.
但這是否有什麼意義呢?未想清楚。。。
------------
訂閱:
文章 (Atom)