上星期想破頭的數論之後,這星期都在看質數相關的Coding。
雖然最終要求的是:$ x^2+y^2 =N $ 的整數解,過程中也回顧了 Eratosthenes's Sieve 求質數表,和用質數表做因式分解 的方法。所用的語言方面,一個目標是自己想要熟習,而且資源又常見的Java;另一個是如果自己在中學時期想這樣做的話,應該會用到的VBA。
Java的例子不少,但試過才知道即使實現的是同一套算法,效率也可以有很大差別。從前只知道應用數學中會看一套算法的Big O去比較時間複雜度,但原來實踐起來用什麼語言、什麼變數物件,結果用什麼什麼形式去表現⋯⋯都會大大影響速度。就是為了找出實際運行得更快的寫法,就一頭栽到這個質數的做法上。雖然一開始時用LinkedList、Map等寫法真的很方便理解,但之後還是儘量換成基本的陣列。
下面這樣的Java寫的 Eratosthenes Sieve 求 一億($10^8$)之內的質數,大約是10秒。如果不計最後一個for loop用來製作傳回值的LinkedList<Integer>的話,主流程大約4秒。不過要求更大的質數,應該還要考慮該程式對使用整數的上限(int: [-2,147,483,648, 2,147,483,647]),大數字在記憶體的儲存方法,整數表的儲存方法等。很多事情都是這樣吧,開始時只要求做到是容易的,但要追求深究下去就會困難⋯⋯
最後還有兩個方法是Modified Eratosthenes Sieve 和 Euler Sieve,都是理論上應該更有效率的算法,不過實踐起來還是達不到應有的分別,要怪我對如何更好地寫代碼還是不熟識吧。 Eratosthenes Sieve的Modification的想法是一開始就不考慮2和3的倍數,只看6k+1和6k+5的情況。至於 Euler Sieve 是改善Eratosthenes Sieve中一個合成數會重覆被質數篩去而浪費的時間,例如,合成數6 會在篩選質數 2和3 的倍數時重覆考慮。理想中Eratosthenes Sieve的時間複雜度是 O( n*log(log(n)) ),而Euler Sieve的時間複雜度是O(n)。實測中,同樣求一億($10^8$)之內的質數,大約是2-3秒的時間。
Bertrand Russell: "Three passions, simple but overwhelmingly strong, have governed my life: the longing for love, the search for knowledge, and unbearable pity for the suffering of mankind."
2016年12月21日 星期三
2016年12月12日 星期一
[Math] 由3個連續數組成的平方和組合 - Consecutive Triple, which are simultaneously sum of 2 squares
前言
先看一下以下數式,有某些數字可以寫成2個平方的和。$
00 = 0^2 + 0^2\\
01 = 1^2 + 0^2\\
02 = 1^2 + 1^2\\
03 = ---..... =3;\\
04 = 2^2 + 0^2\\
05 = 2^2 + 1^2\\
06 = ---...... =2*3\\
07 = ---...... =7\\
08 = 2^2 + 2^2\\
09 = 3^2 + 0^2\\
10 = 3^2 + 1^2 \\
11 = ---..... =11 \\
12 = ---..... =2*2*2*3\\
13 = 3^2 + 2^2\\
14 = ---..... =2*7\\
15 = ---..... =3*5\\
16 = 4^2 + 0^2\\
17 = 4^2 + 1^2\\
18 = 3^2 + 3^2\\
19 = ---..... =19\\
20 = 4^2 + 2^2\\
......\\
$
$
25 = 4^2 + 3^2 = 5^2 + 0^2\\
......\\
65 = 7^2 + 4^2 = 8^2 + 1^2\\
......\\
$
- 某些數字可以寫成2個平方的和,某些則不能,而要寫成更多個平方的和。公元3世紀時的Diophantus提出「是否每一個正整數都是四個平方數之和」的問題。更一般性的問題是 18世紀時的Waring’s problem,他猜想:「對於每個非1的正整數 k,皆存在正整數 g(k),使得每個正整數都可以表示為至多g(k)個k次方數之和。」Diophantus的提問即是當 k=2 的情況 。Lagrange證明了這個情況是 g(2) = 4:任何一個正整數可用4個平方數之和得出。
(e.g. $60=7^2+3^2+1^2+1^2$)
其他情況的證明有 Arthur Wieferich:g(3)=9。Joseph Liouville:g(4)=19。陳景潤:g(5)=37。任何一個正整數可用9個立方數之和、或19個4次方數之和、或37個5次方數之和得出。
- 而對於一個正整數是否可以寫成兩個平方數之和。
首先可留意到上面3、7、11、15、19.... 這些 $(4k+3)$ 的單數項都不能表達成兩個平方數之和。要將一個單數寫成兩個平方之和,兩數必定是一正一負,寫成: $(2k+1)^2 + (2k)^2 = 4(2k^2 + k) + 1$。Fermat首先證明對於單數的質數,可以寫成 (4k+1) 是該數能否寫成兩個平方數之和的充分及必要的條件。 然後,再留意上面寫不到平方和的例子,質因數分解中都出現單數次(4k+3) 形式的質因數項。Euler 證明出以下的條件:
"A number N is expressible as a sum of 2 squares if and only if in the prime factorization of N, every prime of the form (4k+3) occurs an even number of times! "$$N = {2}^{a_0} {p_1}^{2a_1}...{p_r}^{2a_r} {q_1}^{b_1}...{q_s}^{b_s}$$
於是,我們可以分辨出一個數是否可以寫成兩個平方之和。
2016年5月21日 星期六
Edx - TW3421x Credit Risk Management
Edx 上看到一個Credit Risk Management的課堂,報了打算讓自己溫習一下從前上課所學。最近這快要完成了,來總結這課堂所學的內容。
這課堂由Delft University of Technology的Dr. Pasquale Cirillo 講授。說話速度像是刻意放慢了,講解不會沉悶之餘,初時還有用RSA動畫的方式去解釋事情之間關係。內容方面,沒有涉及複雜的數學證明,某些公式出現時就重申:推導過程不在課程以內,然後直接使用。這令課程變得簡單之餘,也清晰了這是集中在讓初學者理解概念。
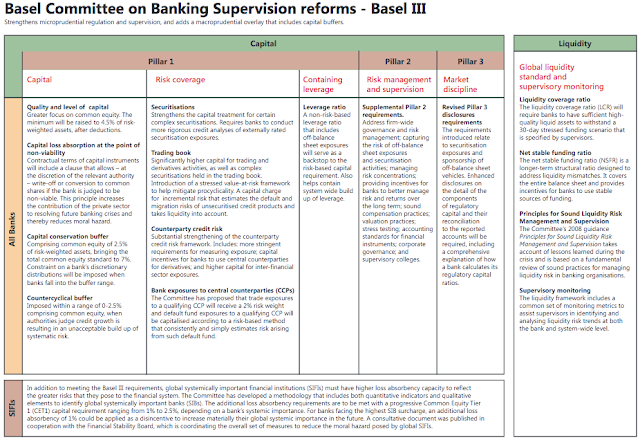
課程把信用風險放在從巴塞爾協定中開始講起。巴塞爾協定是對銀行業的其中一項重要條約。從巴塞爾協定二起,基本定立出三條支柱。
1) Minimum Capital Requirement (Credit Risk, Market Risk, Operational Risk)
2) Supervisory Review Process
3) Market Discipline
更仔細的在:http://www.bis.org/bcbs/basel3/b3summarytable.pdf
這課堂由Delft University of Technology的Dr. Pasquale Cirillo 講授。說話速度像是刻意放慢了,講解不會沉悶之餘,初時還有用RSA動畫的方式去解釋事情之間關係。內容方面,沒有涉及複雜的數學證明,某些公式出現時就重申:推導過程不在課程以內,然後直接使用。這令課程變得簡單之餘,也清晰了這是集中在讓初學者理解概念。
The computation of WCDR is performed using the formula you see on your screen. I do agree with you if you think that this formula has somehow fallen from the sky.
That's true: in this course this formula has fallen from the sky. The point is that, in order to derive this formula completely and formally, we would need - all - a big probabilistic apparatus that we do not have, such as for example the copula model. So, that's it: just take this formula for granted.
課程把信用風險放在從巴塞爾協定中開始講起。巴塞爾協定是對銀行業的其中一項重要條約。從巴塞爾協定二起,基本定立出三條支柱。
1) Minimum Capital Requirement (Credit Risk, Market Risk, Operational Risk)
2) Supervisory Review Process
3) Market Discipline
更仔細的在:http://www.bis.org/bcbs/basel3/b3summarytable.pdf
2016年5月1日 星期日
賭波的初哥方式-Elo Rating System 的理解
之前在未了解背後數學之前先嘗試個應用。今個周未有空就來了解一下Elo Rating System背後是什麼理論,和如何得出那樣的公式了。
Part A)機率
先來看看「邏輯函数」Logistic Function。在很多地方都會看到它的身影,例如物種的人口增長,統計學上的對True/False這類二元結果的回歸分析。
「邏輯函数」 有這樣的一般型式:$$y = \frac{L}{ 1 + e^{-k(x-x_0)} }$$
$e$ :自然對數
$x_0$:x 的中間值
$L$ :y 的最大值
$k$ :斜度
例子一:Standard Logistic Function:$y = \frac{1}{1 + e^{-x}}$
例子二:國際象棋界 USCF 的 Elo rating system 的勝率期望值:$y = \frac{1}{1 + 10^{-\frac{1}{400}(r_A-r_B)}}$
我們考慮代入的是「分數差」(甲的分數-乙的分數), 即是$x=(r_A-r_B)$,$x_0=0$。一個函數可以作為「分數」 與「勝負機率」的轉換,大概很多$\mathbb{R} \to (0,1)$ 的函數都可以做到。而這「邏輯函数」還有以下特質::
「邏輯函数」 在統計模型的重要性在於與「邏輯迴歸」Logistic Regression 的關係。
Logistic Regression Model與一般的「簡單線性迴歸」 Ordinary Linear Regression都是屬於GLM的其中一員,分別在於對「應變數」Dependent Variable的分佈,和所謂的「連結函數」Link Function有不同假設。Logistic Regression Model中,Y 的分佈是要配合"勝/負"這類二元結果, 連結函數的不同就得出機會率可以寫成Logistic Function的形式。Logistic Regression :
$$logit( E [Y | X] ) = ln(\frac{p}{1-p}) = \beta X$$
對觀察值Y的分佈假設為 $Y \sim Binomial (1 , p) $。上式經過移項後會得到:$p = \frac{1}{1 + e^{-\beta X}}$,也就是開始時所見的Logistic Function的形式。
終於,我們回來看看Elo Ratings中的機率公式:
$$S_{expect} = \frac{1}{1 + 10^{-\frac{1}{400}(r_A-r_B)}}$$
Part B)分數
每名棋手會有一個初始分數$r_0$,然隨著實際對賽的結果,用以下公式更新棋手成積:
$$r_{post} = r_{pre} + K (S_{actual} - S_{expect})$$
$r_{post}$:對賽後棋手經調整後的分數。
$r_{pre}$:對賽前棋手原來的分數。
$S_{actual}$:實際結果,簡單可以設定:贏=1分,輸=0分,和=0.5分。
$S_{expect}$:預期結果,就是PartA計算甲會贏的機率公式。
$K$:這一般稱作attenuation factor,是調整新結果的影響和原有分數之間的比重。
一般會有這些考慮:假設比賽結果對新手影響較大,假設重要比賽的影響較大。
因為兩個等級的選手對賽,可以預期分數高的有較大贏面。棋手的分數要值得調整,他應該要表現得超越自己原有等級所預期的水準。Elo Rating更新分數的公式的設計就是為了達到這個效果。
另外,例如有 1200分的棋手A 和 1000分的棋手B 比賽:A,B的預期贏面分別算出是76%, 24%。 A勝出只會增加$0.24K$的分數,B勝出卻會增加$0.74K$的分數。所以:贏(輸)了該贏(輸)的比賽,分數不會有大幅調整;但如果出現戲劇性的結果,分數的調整就會較大。
Part C)應用
這套Elo Rating System在以下幾方面都有被應用:
遊戲:
League Of Legends
http://leagueoflegends.wikia.com/wiki/Elo_rating_system
國際象棋界:
World Chess Federation (FIDE)
https://www.fide.com/fide/handbook.html?id=172&view=article
足球:
World Football Elo Ratings
http://www.eloratings.net/system.html
FIFA Women's World Rankings
http://www.fifa.com/worldranking/procedureandschedule/womenprocedure/index.html
http://resources.fifa.com/mm/document/fifafacts/r%26a-wwr/52/00/99/fs-590_06e_wwr-new.pdf
Footballdatabase.com (雖然無提供背後的模型,但如果沒有數據作自行測試的話也可以一看)
http://footballdatabase.com/ranking/europe/1
因為各方面的比賽有不同特質,所以模型參數略有不同。用以上的 FIFA Women’s World Ranking (WWR) 的模型去看足球方面的實際運作(這裡修改了官方符號方便表示):
$$S_{expect} = 1 / (1 + 10^{x/2})$$
$$ r_{new} = r_{old} + K ( S_{actual} - S_{expect} )$$
文件中稱當中 $x = [r_A - r_B] / (\text{scaling factor})$。scaling factor是為了令新隊伍從1000分開始;對賽中每100分的差距做成64%的的機會勝出。用Excel模擬一下會得到它的scaling factor = -200,所以一樣是這條式:$S_{expect} = 1 / (1 + 10^{-\frac{1}{400}(r_A-r_B)})$



------------
最後一部份,我是懷疑是否有關的,是這套評分和Exponential Distribution的關係。
因為:$A, B \sim Exp(1) \Rightarrow x_0 - \beta ln(A/B) \sim Logistic(x_0, \beta)$
設$R_A, R_B \sim Exp(\dot)$ A,B 是某種實力的量度。Exponential distribution 的圖明顯與Normal Distribution 不同的,它假設選手的$R_A, R_B$ 大多是在低實力區,高手則愈來愈少。它還有一個特點,是分佈上的「無記憶性質」(Memoryless):$Pr(X>m+n|X>m) = Pr(X>n)$ 。對給定的任意一個參考分數而言,比你高同樣n級的比例是一樣的。用一個效果比喻:無論是在哪一級的角色,在下一個等級之前,總是有面前的人當中最弱的3%等著你去超越。
( 以$Exp(1/30)$為例。平均等級是30級。R:pexp(1, rate=1/30) )
設$R_a=ln(R_A), R_b=ln(R_B)$ 。用$ln()$將實力的比例尺轉變成方便比較的分數,$log()$這個運算的起源,是當年在未有計算機的發明之前,有一樣叫對數表的工具,為了方便計算大數的乘法。
$a-b = ln(exp(Ra-Rb)) = ln(exp(Ra)/exp(Rb)) = ln(A/B) \sim Logistic(0,1)$
這就得出分數差會符合Logistic Distribution.
但這是否有什麼意義呢?未想清楚。。。
------------
Part A)機率
先來看看「邏輯函数」Logistic Function。在很多地方都會看到它的身影,例如物種的人口增長,統計學上的對True/False這類二元結果的回歸分析。
「邏輯函数」 有這樣的一般型式:$$y = \frac{L}{ 1 + e^{-k(x-x_0)} }$$
$e$ :自然對數
$x_0$:x 的中間值
$L$ :y 的最大值
$k$ :斜度
例子一:Standard Logistic Function:$y = \frac{1}{1 + e^{-x}}$
例子二:國際象棋界 USCF 的 Elo rating system 的勝率期望值:$y = \frac{1}{1 + 10^{-\frac{1}{400}(r_A-r_B)}}$
我們考慮代入的是「分數差」(甲的分數-乙的分數), 即是$x=(r_A-r_B)$,$x_0=0$。一個函數可以作為「分數」 與「勝負機率」的轉換,大概很多$\mathbb{R} \to (0,1)$ 的函數都可以做到。而這「邏輯函数」還有以下特質::
- 這函數可以輸入實數的「分數差」,而輸出0到1之間的機率值;而且數值是不斷上升的,所以差異愈大,贏(輸)機率就愈大。(這兩個特質就適合用來作"分數差" 和"輸贏機率"之間的轉換)
- 零作為中間點是反向對稱的 $Pr(x)=1-Pr(-x)$,高分方的勝率等於低分方的負率。當雙方實力相等,也就是"分數差"在等於零的時候,輸贏的機率是0.5。
- 而差異愈接近零的時候機率的變化的速度較大;但差異愈大的時候,這個機率的變化速度就愈不明顯。(這個有點像經濟學上「邊際效益遞減」的概念,現實上有點猶豫)
「邏輯函数」 在統計模型的重要性在於與「邏輯迴歸」Logistic Regression 的關係。
Logistic Regression Model與一般的「簡單線性迴歸」 Ordinary Linear Regression都是屬於GLM的其中一員,分別在於對「應變數」Dependent Variable的分佈,和所謂的「連結函數」Link Function有不同假設。Logistic Regression Model中,Y 的分佈是要配合"勝/負"這類二元結果, 連結函數的不同就得出機會率可以寫成Logistic Function的形式。Logistic Regression :
$$logit( E [Y | X] ) = ln(\frac{p}{1-p}) = \beta X$$
對觀察值Y的分佈假設為 $Y \sim Binomial (1 , p) $。上式經過移項後會得到:$p = \frac{1}{1 + e^{-\beta X}}$,也就是開始時所見的Logistic Function的形式。
終於,我們回來看看Elo Ratings中的機率公式:
$$S_{expect} = \frac{1}{1 + 10^{-\frac{1}{400}(r_A-r_B)}}$$
- 從 $e$ 變成 10的次方:因為 $10^x = {e^{ln(10)}}^x =e^{ln(10)x} $,這只是在$k$值的影響。
- $k$:1/400,這個斜度是雙方選手的分數差如何轉換到 0-1的比例上。例如當同樣估計為A勝B,但估計的機率是60%還是70%就是這k值影響到。在線性回歸中我們會用OLS的方法去求取參數,在 Logistic Regression中參數是用「最大似然估計」Maximum Likelihood Estimation (MLE)找出來。
- $r_A, r_B$:選手的分數,這裡並不是一個可以直接觀察到的自變數,如何得出這分數就是Elo Rating 的另一重要部份。
Part B)分數
每名棋手會有一個初始分數$r_0$,然隨著實際對賽的結果,用以下公式更新棋手成積:
$$r_{post} = r_{pre} + K (S_{actual} - S_{expect})$$
$r_{post}$:對賽後棋手經調整後的分數。
$r_{pre}$:對賽前棋手原來的分數。
$S_{actual}$:實際結果,簡單可以設定:贏=1分,輸=0分,和=0.5分。
$S_{expect}$:預期結果,就是PartA計算甲會贏的機率公式。
$K$:這一般稱作attenuation factor,是調整新結果的影響和原有分數之間的比重。
一般會有這些考慮:假設比賽結果對新手影響較大,假設重要比賽的影響較大。
因為兩個等級的選手對賽,可以預期分數高的有較大贏面。棋手的分數要值得調整,他應該要表現得超越自己原有等級所預期的水準。Elo Rating更新分數的公式的設計就是為了達到這個效果。
另外,例如有 1200分的棋手A 和 1000分的棋手B 比賽:A,B的預期贏面分別算出是76%, 24%。 A勝出只會增加$0.24K$的分數,B勝出卻會增加$0.74K$的分數。所以:贏(輸)了該贏(輸)的比賽,分數不會有大幅調整;但如果出現戲劇性的結果,分數的調整就會較大。
Part C)應用
這套Elo Rating System在以下幾方面都有被應用:
遊戲:
League Of Legends
http://leagueoflegends.wikia.com/wiki/Elo_rating_system
國際象棋界:
World Chess Federation (FIDE)
https://www.fide.com/fide/handbook.html?id=172&view=article
足球:
World Football Elo Ratings
http://www.eloratings.net/system.html
FIFA Women's World Rankings
http://www.fifa.com/worldranking/procedureandschedule/womenprocedure/index.html
http://resources.fifa.com/mm/document/fifafacts/r%26a-wwr/52/00/99/fs-590_06e_wwr-new.pdf
Footballdatabase.com (雖然無提供背後的模型,但如果沒有數據作自行測試的話也可以一看)
http://footballdatabase.com/ranking/europe/1
因為各方面的比賽有不同特質,所以模型參數略有不同。用以上的 FIFA Women’s World Ranking (WWR) 的模型去看足球方面的實際運作(這裡修改了官方符號方便表示):
$$S_{expect} = 1 / (1 + 10^{x/2})$$
$$ r_{new} = r_{old} + K ( S_{actual} - S_{expect} )$$
文件中稱當中 $x = [r_A - r_B] / (\text{scaling factor})$。scaling factor是為了令新隊伍從1000分開始;對賽中每100分的差距做成64%的的機會勝出。用Excel模擬一下會得到它的scaling factor = -200,所以一樣是這條式:$S_{expect} = 1 / (1 + 10^{-\frac{1}{400}(r_A-r_B)})$

- 它們對模型的修改上考慮到入球數目的不同:

- 主場的優勢:主隊加100分
"A glance at the historical results shows that teams perform better at home than away; the home teams keep 66% of the points, while the opponents return home with 34%. To neutralise this effect, a correction is made by enhancing the rating of the home team by a value of 100 points (corresponding to 64%)."
- 對於賽事重要性:

- 參考的時間歷史:45年的比賽紀錄,在評分的角度上還可以接受,但我覺得對勝負機會率的目的來說就太多。現在的球隊隊員跟好幾年前的早就不同了吧。
"Solid foundation: some 6500 games since 1971"
- 開始評分所需的數據:其實我覺得這套方式比較適合LOL遊戲平台上的計分,那時每次分數更新反映的是一個學習過程。但在象棋/足球這類大量練習,然後參加一場聯賽的情況中,每次分數更新就像是尋求反映真正實力的過程,這就要有足夠對實往績能達到效果。事實上,也因為Logistic Regression 的參數是用到MLE的方法,一般需要的樣本數也要較大。
"The ranking of a team is deemed official when:They have played at least 5 matches against teams with an official ranking. etc..."
------------
最後一部份,我是懷疑是否有關的,是這套評分和Exponential Distribution的關係。
因為:$A, B \sim Exp(1) \Rightarrow x_0 - \beta ln(A/B) \sim Logistic(x_0, \beta)$
設$R_A, R_B \sim Exp(\dot)$ A,B 是某種實力的量度。Exponential distribution 的圖明顯與Normal Distribution 不同的,它假設選手的$R_A, R_B$ 大多是在低實力區,高手則愈來愈少。它還有一個特點,是分佈上的「無記憶性質」(Memoryless):$Pr(X>m+n|X>m) = Pr(X>n)$ 。對給定的任意一個參考分數而言,比你高同樣n級的比例是一樣的。用一個效果比喻:無論是在哪一級的角色,在下一個等級之前,總是有面前的人當中最弱的3%等著你去超越。
( 以$Exp(1/30)$為例。平均等級是30級。R:pexp(1, rate=1/30) )
設$R_a=ln(R_A), R_b=ln(R_B)$ 。用$ln()$將實力的比例尺轉變成方便比較的分數,$log()$這個運算的起源,是當年在未有計算機的發明之前,有一樣叫對數表的工具,為了方便計算大數的乘法。
$a-b = ln(exp(Ra-Rb)) = ln(exp(Ra)/exp(Rb)) = ln(A/B) \sim Logistic(0,1)$
這就得出分數差會符合Logistic Distribution.
但這是否有什麼意義呢?未想清楚。。。
------------
2016年4月25日 星期一
賭波的初哥方式一檢討
八強賽事完結,結果是不好的了。但這初哥當初決定放入少許注碼,希望投入到去體驗,實際地知道到了什麼:
1. 注碼佔口袋裡錢的比例要更少。當一注是本金的 1x - 20%,輸幾注就感覺很危險。
(這是不符合Kelly Criteria嗎?原來是自己用錯賠率了)
2. Kelly Criteria 用的是淨賠率,是馬會顯示的賠率-1。
(其實修正過後大部份場都不值得下注。這可能是低估了機會率,或馬會的給的賠率太低了。)
3. 足球不能簡化為勝負二個賽果。在一般的:主、客、和。當兩隊實力相約,和的機率其實不少,不能不考慮打和。而且相比單純贏輸幾球,最好可以有估波膽形式般的預測,這樣才能享用較高賠率。
4. 可以分開:得、失球 的能力,有人用過去的Poisson Distribution作工具,這應該可以考慮加入得失球分開的辦法。 或 之前的Least square estimation也應該這樣。而且這類方法目標是要有機率,要知誤差。
5. 要了解ELO背後模型,如何才能用在主客和3種情況。ELO的初始參數要做校準,去調整合適的機會率和界線。
---------------------------
這些有的是八強首圈時發現的,但還未花時間研究如何修改。下一場快上演了,更重要的是不能拖著自己寫Blog的進度。
1. 注碼佔口袋裡錢的比例要更少。當一注是本金的 1x - 20%,輸幾注就感覺很危險。
(這是不符合Kelly Criteria嗎?原來是自己用錯賠率了)
2. Kelly Criteria 用的是淨賠率,是馬會顯示的賠率-1。
(其實修正過後大部份場都不值得下注。這可能是低估了機會率,或馬會的給的賠率太低了。)
3. 足球不能簡化為勝負二個賽果。在一般的:主、客、和。當兩隊實力相約,和的機率其實不少,不能不考慮打和。而且相比單純贏輸幾球,最好可以有估波膽形式般的預測,這樣才能享用較高賠率。
4. 可以分開:得、失球 的能力,有人用過去的Poisson Distribution作工具,這應該可以考慮加入得失球分開的辦法。 或 之前的Least square estimation也應該這樣。而且這類方法目標是要有機率,要知誤差。
5. 要了解ELO背後模型,如何才能用在主客和3種情況。ELO的初始參數要做校準,去調整合適的機會率和界線。
---------------------------
這些有的是八強首圈時發現的,但還未花時間研究如何修改。下一場快上演了,更重要的是不能拖著自己寫Blog的進度。
2016年3月31日 星期四
賭波的初哥方式-Least Square Estimation & Elo Rating System
星期三放假在家,空閒的時間再嘗試一下去年的足球博彩模型。當時因為自己讀過點數學和統計,一直想有點實際的應用;朋友V想用模型預測球賽結果和博彩,而我工作時又會弄點程式來方便日常工作,所以去年就和我嘗試提高預測球賽結果的賺錢機會,以及做點自動化的工具。
去年,加入的是一個為每隊評分的方法。假設每隊有一個代表綜合實力的分數-Rating,而得失球的差-Score只是兩隊分數的差。用過往每隊的對賽結果,放入一個方程組(System of Linear Equations) $\underline{HA \times teamRank=Score}$ 去求最小方差(Least square estimation)的解,就可以反求出這些分數。
$$
\begin{bmatrix}
1 & 0 & 0 & -1 \\
0 & 1 & -1 & 0 \\
-1 & 0 & 1 & 0 \\
0 & -1 & 0 & 1 \\
0 & 0 & -1 & 1 \\
-1 & 1 & 0 & 0 \\
0 & 0 & 1 & -1 \\
1 & -1 & 0 & 0 \\
1 & 0 & 0 & -1 \\
-1 & 0 & 0 & 1 \\
0 & -1 & 1 & 0 \\
0 & 1 & 0 & -1 \\
0 & 1 & 0 & -1 \end{bmatrix}
\times
\begin{bmatrix}
1.375 \\
2 \\
-2.5 \\
-0.875 \end{bmatrix}
=
\begin{bmatrix}
2 \\
8 \\
-5 \\
-1 \\
4 \\
1 \\
1 \\
0 \\
-3 \\
-2 \\
2 \\
4 \end{bmatrix}$$
當然,我們想做的是把這些運算交給電腦。當只要做好數據的準備,在R上除了數據的輸入和顯示外,重要的運算就只是一行Coding:
去年,加入的是一個為每隊評分的方法。假設每隊有一個代表綜合實力的分數-Rating,而得失球的差-Score只是兩隊分數的差。用過往每隊的對賽結果,放入一個方程組(System of Linear Equations) $\underline{HA \times teamRank=Score}$ 去求最小方差(Least square estimation)的解,就可以反求出這些分數。
$$
\begin{bmatrix}
1 & 0 & 0 & -1 \\
0 & 1 & -1 & 0 \\
-1 & 0 & 1 & 0 \\
0 & -1 & 0 & 1 \\
0 & 0 & -1 & 1 \\
-1 & 1 & 0 & 0 \\
0 & 0 & 1 & -1 \\
1 & -1 & 0 & 0 \\
1 & 0 & 0 & -1 \\
-1 & 0 & 0 & 1 \\
0 & -1 & 1 & 0 \\
0 & 1 & 0 & -1 \\
0 & 1 & 0 & -1 \end{bmatrix}
\times
\begin{bmatrix}
1.375 \\
2 \\
-2.5 \\
-0.875 \end{bmatrix}
=
\begin{bmatrix}
2 \\
8 \\
-5 \\
-1 \\
4 \\
1 \\
1 \\
0 \\
-3 \\
-2 \\
2 \\
4 \end{bmatrix}$$
當然,我們想做的是把這些運算交給電腦。當只要做好數據的準備,在R上除了數據的輸入和顯示外,重要的運算就只是一行Coding:
以2013-2014年度英超對賽的紀錄作計算,最好幾隊分別是:teamRank = ginv(HA) %*% score;
- 曼城=1.625
- 利物浦=1.275
- 車路士=1.1
- 阿仙奴=0.675
- 愛華頓=0.55
2016年2月28日 星期日
[Math] Office Work - Single Precision Error from Decimal to Floating
電腦是以1、0表示所有資料,基本如數字也是這樣,為了在同樣容量下儲存更多或更準確的數字,便先要指定格式。例如以32Bit的單位下,如果我們想記錄「整數」,先有1 Bit用了表示正負數,餘下的31 Bit就只可以記錄$2^{31}$個數,所以32 Bit最大的正整數是$2^{31}-1 = 2147483647$。如果電腦要紀錄更大的數值,就要指定要其他的儲存容量(例如Long Integer:用多一倍的單位64Bits)或其他的儲存方式(例如Float:$1.0 \times 2^{128}$)。
以印尼银行(Bank Indonesia - 印尼的中央銀行)的印尼盾匯率為例:印行會用當日雅加達時間上午8.00-9.45銀行間同業交易的USD/IDR即期匯率,計算加權平均,然後在上午10.00公佈該這個參考價-雅加達銀行同業即期匯率(JISDOR),和現時22種貨幣的參考匯率,發佈的數字只有買入價、賣出價,並沒有中間價。
要知道一般大眾看的就是中間價。談到日元歐元下跌又是旅行良機時,你不會分別說買入賣出價是多少。某數據供應商亦合理地有提供中間價 ( =(買入+賣出)/2 )。只是,數據商預設準確至2個小數位(2 d.p.) ,當我們留意這個數據的準確性時,卻偶然出現細小的誤差,例如:
以印尼银行(Bank Indonesia - 印尼的中央銀行)的印尼盾匯率為例:印行會用當日雅加達時間上午8.00-9.45銀行間同業交易的USD/IDR即期匯率,計算加權平均,然後在上午10.00公佈該這個參考價-雅加達銀行同業即期匯率(JISDOR),和現時22種貨幣的參考匯率,發佈的數字只有買入價、賣出價,並沒有中間價。
要知道一般大眾看的就是中間價。談到日元歐元下跌又是旅行良機時,你不會分別說買入賣出價是多少。某數據供應商亦合理地有提供中間價 ( =(買入+賣出)/2 )。只是,數據商預設準確至2個小數位(2 d.p.) ,當我們留意這個數據的準確性時,卻偶然出現細小的誤差,例如:
2016年2月20日 星期六
[Math] Office Work - 從編排更表到Hungarian Algorithm
因為會處理歐美收市和亞洲收市,所以我這組人的繁忙時間是清早和晚上兩端,需要有輪班制,工作分早晚兩更,據英文堂所學這種工作時間有個形容詞是antisocial hour, 人手足夠時就可以讓同事返九點左右的正常時間。編更上如何令大家滿意,這問題幾似數學Operational Research / Graph Theory中的 Matching problem。大概最近FB見到恆隆同伯賴段片,數學應用的頭腦靈活過來,想到還是可以用典型的Hungarian Algorithm。這演算法所處理的情況是:假設有n個任務需要分派給n個人,每人要完成各個任務都有某個成本,問如何編配任務才能讓總成本最少。
例如成員 i 要處理任務 j 的成本是cij,這些成本可以寫成矩陣C表示。例如第一個人p1處理任務一task1要成本1, p1 處理 task2 要成本5, p1 處理 task3 要成本3;分派方法可以寫成矩陣A,這簡單例子的最佳分配可以直觀得知如下, 總成本為6。而Hungarian Algorithm 的步驟是這樣,大致有以下程序:(一)將所有數值減去該行最小的數,然後再將所有數值減去該列最小的數,今每行、列都有零存在。(二)[Trial and Error] 找出一個"Independent zero"的組合,用最少條線穿過所有零。(三)如果剛好存在於n條線上,該"Independent zero"組合就可以得出答案;如果只需少過n條線,修改矩陣重覆步驟二。
$$
C=\begin{bmatrix}
1 & 5 & 3 \\
4 & 2 & 8 \\
7 & 9 & 3 \end{bmatrix},
A=\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \end{bmatrix}
$$
例如成員 i 要處理任務 j 的成本是cij,這些成本可以寫成矩陣C表示。例如第一個人p1處理任務一task1要成本1, p1 處理 task2 要成本5, p1 處理 task3 要成本3;分派方法可以寫成矩陣A,這簡單例子的最佳分配可以直觀得知如下, 總成本為6。而Hungarian Algorithm 的步驟是這樣,大致有以下程序:(一)將所有數值減去該行最小的數,然後再將所有數值減去該列最小的數,今每行、列都有零存在。(二)[Trial and Error] 找出一個"Independent zero"的組合,用最少條線穿過所有零。(三)如果剛好存在於n條線上,該"Independent zero"組合就可以得出答案;如果只需少過n條線,修改矩陣重覆步驟二。
$$
C=\begin{bmatrix}
1 & 5 & 3 \\
4 & 2 & 8 \\
7 & 9 & 3 \end{bmatrix},
A=\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \end{bmatrix}
$$
訂閱:
文章 (Atom)